Was ist ISO 2768? Ein Leitfaden für Toleranzstandards in der CNC-Fertigung
Die Herstellung eines Teils ohne Abweichungen vom ursprünglichen Entwurf ist äußerst kompliziert. Selbst wenn Sie ein Exemplar erhalten können, das der Designabsicht ähnelt, ist es fast unmöglich, in einem Serienprozess immer die gleichen exakten Abmessungen zu erreichen. Sie können jedoch festlegen, wie stark ein gefertigtes Teil vom ursprünglichen Entwurf abweichen darf, um akzeptiert zu werden. In der Fertigung wird dieser Akzeptanzbereich durch Grenzwerte bestimmt, die als Toleranzgrenzen bezeichnet werden. Diese Toleranzen stellen die Abweichungen zwischen den Nennmaßen (ursprüngliche Absicht des Entwurfs) und den Höchst- und Mindestwerten eines Maßes dar, die noch einen angemessenen Entwurf gewährleisten; oder einfach ausgedrückt, eine kontrollierte Fehlerspanne. Nehmen wir an, Sie spezifizieren eine runde, massive Stange von 100 mm Länge mit Ø50 mm, die in ein Loch eines anderen Teils passt. Sie geben einen Auftrag zur Herstellung von 200 dieser Rundstäbe mit Ø50 mm. Als Sie die Stäbe erhalten, stellen Sie fest, dass sie nicht alle Ø50 mm messen, sondern dass Sie Werte wie Ø53 mm, Ø47 mm, Ø51 mm, Ø49 mm erhalten, mit einer großen Abweichung. Die Stäbe variieren auch in der Länge und wenn Sie genau hinsehen, stellen Sie fest, dass sie nicht perfekt rund sind. Können Sie sie noch verwenden? Wenn nicht, können Sie sie zurückweisen und den Lieferanten bitten, sie kostenlos nachzufertigen? Wie nah an Ø50 mm sollten sie wirklich sein?
ISO 2768: eine internationale Norm
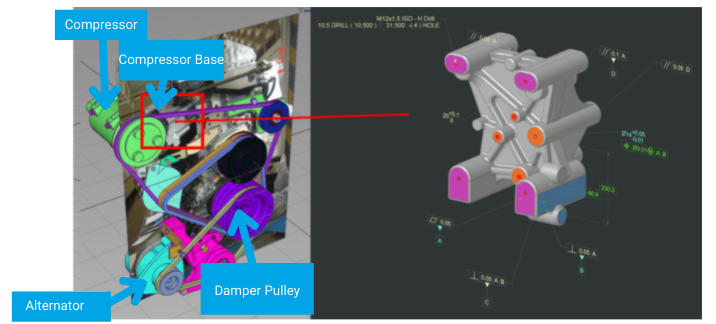
Es gibt einen internationalen Standard, der nicht nur hilft, diese Fragen zu beantworten, sondern auch dazu beiträgt, Unstimmigkeiten zu minimieren und gleichzeitig die Produktionskosten zu berücksichtigen. Und das Beste daran: Da er von einem internationalen Komitee erstellt wurde, stehen Sie auf der gleichen Seite wie Unternehmen auf der ganzen Welt, so dass es keine Missverständnisse gibt. Diese Norm ist die ISO 2768. Um den Inhalt dieser Norm und ihre Bestandteile zu erklären, werden wir ein reales technisches Beispiel verwenden. Abbildung 1 zeigt einen Fahrzeugmotor mit einem Klimakompressor. Das Teil, das den Kompressor trägt und ihn mit dem Motor verbindet, ist für uns von zentraler Bedeutung; wir nennen es die „Kompressorbasis“. Wir beginnen mit einem Prototyp aus Aluminium, der dann bearbeitet und gebohrt wird.
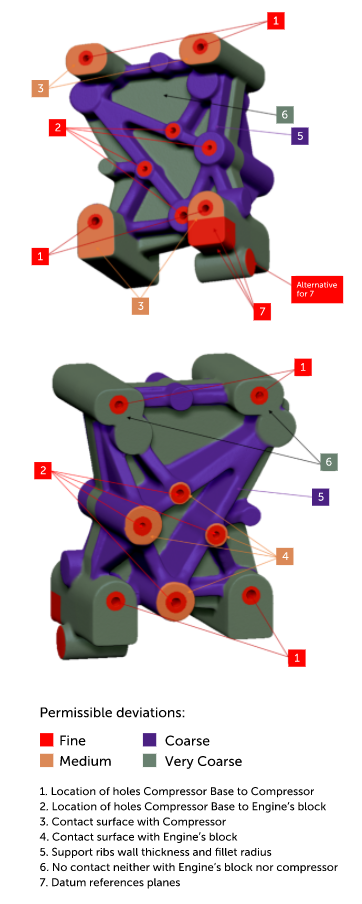
Sobald ein 3D-Modell mit Nennmaßen definiert ist, bestimmen wir, welche Merkmale enge Toleranzen erfordern und welche stärker abweichen dürfen, damit wir diese Anforderungen auf der 2D-Arbeitszeichnung angeben können. Der Grund für die Differenzierung der Toleranzniveaus ist einfach: Wenn alle Abmessungen enge Toleranzen erfordern, steigen die Kosten des Teils aufgrund der anspruchsvolleren Werkzeuge/Vorrichtungen, der Fähigkeiten der Bediener und der Anforderungen an Ausschuss/Nacharbeit erheblich. Auch die Lieferzeit erhöht sich, da jedes Teil in der Charge eine strenge Qualitätskontrolle erfordert, um jede Abmessung zu bestätigen. Und wie in diesem Beispiel gezeigt, haben einige Komponenten komplexe zusammengesetzte Geometrien, die sich nicht einfach quantifizieren lassen. Bei der Konstruktion eines Bauteils ist es wichtig, sich zu fragen, welche Hauptfunktion die einzelnen Merkmale haben. Einige Abmessungen können kritisch sein, weil sie mit anderen Teilen ausgerichtet werden sollen, daher muss die Fehlermarge kontrolliert werden. Andererseits gibt es Merkmale mit Abmessungen und Positionen, die nicht so kritisch sind, so dass sie bei der Herstellung flexibler sein können. Wie Sie sich denken können, ist es ein Kompromiss zwischen Genauigkeit und Kosten. Für unser Beispiel des Kompressorsockels zeigt Abbildung 2, welche Features eigentlich eine enge Toleranz haben sollten und welche mehr variieren dürfen. Beachten Sie, dass die dargestellte Klassifizierung als Beispiel gedacht ist und daher von anderen Designs abweichen kann. Es liegt in Ihrer Verantwortung, eine geeignete Klassifizierung auf der Grundlage der Funktion Ihres Produkts zu entwickeln. In unserem Fall müssen die Bohrungen für die Verbindung mit dem Motorblock und dem Kompressor ausgerichtet und korrekt positioniert sein, daher fällt ihre Toleranz in die Kategorie fein (siehe #1 und #2 in Abbildung 2). Die Kontaktflächen zwischen den Komponenten sind ebenfalls wichtig für die Ausrichtung (#3 und #4), aber für dieses spezielle Beispiel konnten wir eine mittlere Toleranz verwenden, da eine genauere Maschinenrauheit als die, die wir vom Lieferanten erhalten haben, keine ausreichende Ausrichtung ermöglichte, um die zusätzlichen Kosten zu rechtfertigen. Andererseits dienen die Rippen der Festigkeit, so dass ihre Wandstärke mit einem akzeptablen Mindestwert mit einer weniger strengen Toleranz definiert werden kann, solange sie die untere Grenze einhält (#5, grobe Toleranz). Der Hauptteil der Basis wurde mit einer sehr groben Toleranz definiert (#6) und schließlich definieren wir Referenzflächen oder Bezugspunkte, um den Rest der Abmessungen zu kontrollieren (#7, feine Toleranz, da wir von diesen Flächen aus messen). Denken Sie daran, dass bei anderen Entwürfen Merkmale wie Rippen, Verrundungen und Fasen je nach ihrer Funktion entscheidend sein können.
ISO 2768 ist in zwei Teile unterteilt, die beide zur Vereinfachung von Zeichnungen beitragen, indem sie Präzisionsstufen als allgemeine Regeln definieren:
- Allgemeintoleranzen für Längen- und Winkelmaße (Teil 1) mit den Präzisionsstufen: f-fein, m-mittel, c-grob, v-sehr grob
- Geometrische Toleranzen für Objekte (Teil 2) mit Präzisionsstufen, die als Toleranzklassen definiert sind: H, K und L
Eine 2D-Arbeitszeichnung kann beispielsweise als ISO2768-mK spezifiziert werden, was bedeutet, dass sie in der Regel die Toleranzbereiche für „mittel“ in Teil 1 und die Toleranzklasse „K“ in Teil 2 einhalten muss. Indem Sie die ISO2768-Spezifikation einbeziehen, vereinfachen Sie die Zeichnung und vermeiden es, Toleranzen für jedes Maß und jede Funktion zu schreiben. Wir haben die allgemeine Regel erwähnt, weil es Ausnahmen geben kann, wenn ein Maß eine engere Toleranz als die der ISO2768 benötigt. Das ist normal und üblich. Achten Sie also immer auf das Schriftfeld der Zeichnung, um allgemeine Toleranzanforderungen zu ermitteln und bleiben Sie dran, wenn es eine spezielle Teilespezifikation oder Projektanforderung gibt. Sie sollten sich auch darüber im Klaren sein, dass es mehrere andere Normen gibt, die mit ähnlichen Abmessungskonzepten arbeiten.
ISO 2768 Teil 1: Lineare und winklige Abmessungen
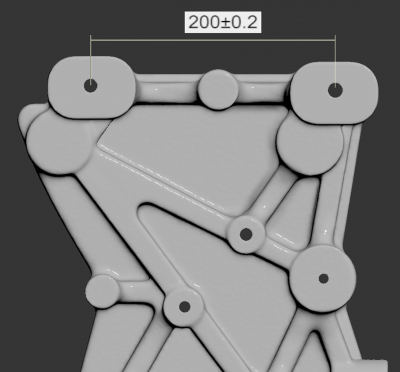
Tabelle 1 zeigt die Genauigkeitsstufen oder Toleranzklassen für lineare Maße. Eine Anwendung ist das Maß zwischen den Bohrungen für unser Beispiel eines Kompressorsockels (siehe Abbildung 3).
Tabelle 1: Toleranzklassen – lineare Abmessungen
| Zulässige Abweichungen in mm | ||||
| Grundgrößenbereich in mm | f (fein) | m (mittel) | c (grob) | v (sehr grob) |
| 0,5 bis 3 | ±0.05 | ±0.1 | ±0.2 | – |
| von 3 bis 6 | ±0.05 | ±0.1 | ±0.3 | ±0.5 |
| von 6 bis 30 | ±0.1 | ±0.2 | ±0.5 | ±1.0 |
| von 30 bis 120 | ±0.15 | ±0.3 | ±0.8 | ±1.5 |
| von 120 bis 400 | ±0.2 | ±0.5 | ±1.2 | ±2.5 |
| von 400 bis 1000 | ±0.3 | ±0.8 | ±2.0 | ±4.0 |
| von 1000 bis 2000 | ±0.5 | ±1.2 | ±3.0 | ±6.0 |
| von 2000 bis 4000 | – | ±2.0 | ±4.0 | ±8.0 |
In ähnlicher Weise zeigt Tabelle 2 die Toleranzen für Außenradien und Fasen.
Tabelle 2: Toleranzklassen – Außenradien und Fasen
| Zulässige Abweichungen in mm | ||||
| Grundgrößenbereich in mm | f (fein) | m (mittel) | c (grob) | v (sehr grob) |
| 0,5 bis 3 | ±0.2 | ±0.2 | ±0.4 | ±0.4 |
| von 3 bis 6 | ±0.5 | ±0.5 | ±1.0 | ±1.0 |
| von 6 | ±1.0 | ±1.0 | ±2.0 | ±2.0 |
Und um Teil 1 der ISO 2768 zu vervollständigen, haben wir Tabelle 3, die die Toleranzen für Winkelmaße definiert. Beachten Sie, dass die Toleranzeinheiten in Tabelle 3 Grad und Minuten sind, wie für ein Winkelmaß zu erwarten. In Teil 2 werden wir ein neues Konzept namens „Rechtwinkligkeit“ definieren, dessen Einheiten tatsächlich die Länge (mm) sind, obwohl es zwei Oberflächen in einem Winkel kontrolliert.
Tabelle 3: Toleranzklassen – Winkelmaße
| Zulässige Abweichungen in mm | ||||
| Grundgrößenbereich in mm | f (fein) | m (mittel) | c (grob) | v (sehr grob) |
| bis zu 10 | ±1º | ±1º | ±1º30′ | ±3º |
| von 10 bis 50 | ±0º30′ | ±0º30′ | ±1º | ±2º |
| von 50 bis 120 | ±0º20′ | ±0º20′ | ±0º30′ | ±1º |
| von 120 bis 400 | ±0º10′ | ±0º10′ | ±0º15′ | ±0º30′ |
| von 400 | ±0º5′ | ±0º5′ | ±0º10′ | ±0º20′ |
ISO 2768 Teil 2: Geometrische Toleranzen für Merkmale
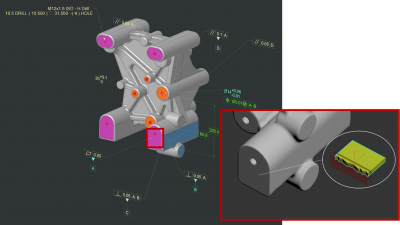
Teil 2 definiert drei Toleranzbereiche H, K und L. Diese unterscheiden sich von den Montage- und Spieltoleranzklassen, die ebenfalls Buchstaben und Zahlen verwenden. Wie in Teil 1 haben wir Nennbereiche und Abweichungen, aber der Unterschied besteht darin, wie wir diese Abweichungen definieren. Ein Beispiel finden Sie in Abbildung 4: Anstatt eine Ober- und eine Untergrenze zu definieren, legen wir einen Bereich zwischen zwei Referenzen (d.h. parallelen Ebenen) fest, so dass die gefertigte Oberfläche in diesem Bereich liegen muss. Das hört sich vielleicht komplizierter an, macht aber tatsächlich Sinn, wenn Sie ein Teil messen und feststellen, dass Sie, wenn Sie einen Messschieber zum Messen zweier rauer Oberflächen ansetzen, aufgrund der Rauheit der Oberflächen unterschiedliche Messwerte erhalten werden. Wir legen Nullpunkte fest, die wir als Referenz für die Abmessungen verwenden und um zu bestimmen, wie viel Abweichung akzeptabel ist. Wie in Abbildung 2 dargestellt, haben wir drei senkrechte Flächen für den Basiskompressor gewählt (Bezugspunkt A, B, C in Abbildung 1).
Tabelle 4 definiert die Toleranzklassen für Ebenheit und Geradheit. Eine Oberfläche kann eine übermäßige Rauheit aufweisen. Bei unserem Kompressorsockel sind die Kontaktflächen zwischen dem Kompressor und dem Sockel sowie die Kontaktflächen zwischen dem Sockel und dem Motor wichtig, daher wird ihre Ebenheit in der Zeichnung angegeben. Die Geradheit bestimmt, wie stark eine Oberfläche innerhalb einer bestimmten Linie auf dieser Oberfläche variiert. Die Geradheit wird auch für die Achse eines Teils verwendet, um zu bestimmen, wie stark es sich biegen oder drehen darf.
Tabelle 4: Toleranzen für Geradheit und Ebenheit
| Zulässige Abweichungen in mm | |||
| Grundgrößenbereich in mm | H | K | L |
| bis zu 10 | 0.02 | 0.05 | 0.1 |
| von 10 bis 30 | 0.05 | 0.1 | 0.2 |
| von 30 bis 100 | 0.1 | 0.2 | 0.4 |
| von 100 bis 300 | 0.2 | 0.4 | 0.8 |
| von 300 bis 1000 | 0.3 | 0.6 | 1.2 |
| von 1000 bis 3000 | 0.4 | 0.8 | 1.6 |
Wie bereits erwähnt, hat die Rechtwinkligkeit Abstandseinheiten in mm. Ähnlich wie bei der Ebenheit definieren wir zwei Ebenen, die durch einen Abstand getrennt sind, der der zulässigen Abweichung in Tabelle 5 entspricht. Wir kontrollieren den 90-Grad-Winkel indirekt, da wir messen, ob die Oberfläche im zulässigen Bereich liegt (siehe Abbildung 6)
| Zulässige Abweichungen in mm | |||
| Bereich der Nennlängen in mm (kurze Seite) | H | K | L |
| bis zu 100 | 0.2 | 0.4 | 0.6 |
| von 100 bis 300 | 0.3 | 0.6 | 1 |
| von 300 bis 1000 | 0.4 | 0.8 | 1.5 |
| von 1000 bis 3000 | 0.5 | 0.8 | 2 |
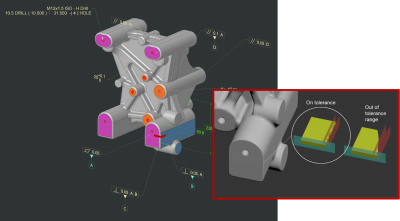
Abbildung 6: Beispiel für eine rechtwinklige Kompressionsbasis. Beachten Sie, dass eine Fläche, die zwischen den beiden roten Ebenen liegt, in einem Bereich liegt, der senkrecht zur blauen Referenzebene ist, aber wenn sie außerhalb der Toleranz liegt, ist der Winkel zwischen der Fläche und dem Nullpunkt deutlicher
Tabelle 6 zeigt Symmetrietoleranzen – zulässige Abweichungen für zwei Objekte auf einem Teil, die über eine Bezugsebene gleich sind.
Tabelle 6: Toleranzen für die Symmetrie
| Zulässige Abweichungen in mm | |||
| Bereich der Nennlängen in mm | H | K | L |
| bis zu 100 | 0.5 | 0.6 | 0.6 |
| von 100 bis 300 | 0.5 | 0.6 | 1 |
| von 300 bis 1000 | 0.5 | 0.8 | 1.5 |
| von 1000 bis 3000 | 0.5 | 1 | 2 |
Und die letzte Tabelle in Teil 2 entspricht dem Rundlauf, d.h. der gesamten Abweichung, die eine Oberfläche haben kann, wenn das Teil um die Achse eines Nullpunkts gedreht wird. Beachten Sie, dass die markierte Fläche innerhalb der Toleranz liegt, obwohl sie nicht perfekt zylindrisch ist.
Tabelle 7: Auslass-Toleranzen
| Zulässige Abweichungen in mm | |||
| Kreisförmiger Auslauf | H | K | L |
| – | 0.1 | 0.2 | 0.5 |
Sie haben vielleicht bemerkt, dass es keine Tabelle für die Parallelität gibt. Das liegt daran, dass ISO2768 Teil 2 die Parallelität als gleich dem numerischen Wert der Größentoleranz oder der Ebenheits-/Geradheitstoleranz definiert, je nachdem, welcher Wert größer ist. Beide Toleranzen werden weiter oben in diesem Artikel behandelt.
Schlussfolgerung und nächste Schritte
Die ISO 2768 behandelt einige der in der Industrie verwendeten Toleranz- und geometrischen Merkmale und ist ein guter Ausgangspunkt. Es gibt jedoch noch weitere Normen, die sich auf das Konzept der geometrischen Bemaßung und Toleranzen (GD&T) erstrecken, deren Symbole in Tabelle 8 aufgeführt sind. Mehrere Unternehmen haben eine Methode namens Model Based Definition (MBD) eingeführt, um die Zusammenarbeit zu verbessern, indem sie alle GD&T-, Toleranz- und Datumsinformationen in 3D-Modelle anstelle von 2D-Zeichnungen aufnehmen. Theoretisch ist dies möglich, da einige CAD-Programme über Werkzeuge verfügen, die diese Symbole und Werte als parametrische Informationen enthalten. Ich persönlich bin der Meinung, dass die Ersetzung von 2D-Zeichnungen durch 3D-Modelle als Standard eingeführt werden sollte, aber wer weiß, ob und wann dies geschieht? Das Ingenieurwesen entwickelt sich ständig weiter.
Tabelle 8: GD & T Begriffe
| Art der Kontrolle | Geometrische Merkmale | Symbol |
| Form | Geradheit |  |
| Form | Ebenheit |  |
| Form | Rundheit |  |
| Form | Zylindrizität |  |
| Profil | Profil einer Linie |  |
| Profil | Profil einer Oberfläche |  |
| Orientierung | Rechtwinkligkeit |  |
| Ausrichtung | Winkligkeit |  |
| Ausrichtung | Parallelität |  |
| Standort | Symmetrie |  |
| Standort | Wahre Position |  |
| Standort | Konzentrizität |  |
| Auslauf | Auslauf |  |
| Rundlauf | Total Runout |  |